Kryptografií rozumíme šifrování a dešifrování (encryption and decryption) posílaných zpráv, tedy snahu poslat zprávu, která bez dešifrovacího klíče nedává smysl.
Kryptografie je mnohem starší než IT, byla potřeba především během válečných konfliktů.
V současné době většina komunikace jde vzduchem → odposlouchávání → nutnost komunikaci šifrovat.
Na principu šifrování a dešifrování také fungují další ochranné mechanismy, např. ověření hesla, certifikátu, digitálního podpisu…
Úsilí o „dokonalou“ šifru vede k hlubšímu využití teorie čísel a pravděpodobnosti.
Co je to kryptografie?
- Kryptografie začíná, když místo hmotných zámků použijeme šifry.
- Umožní nám zakódovat zprávy, které nebudou dávat ostatním smysl.
- Vyžaduje abychom porozuměli myšlenkám spojených s teorií čísel a pravděpodobností.
Využití kryptografie v praxi
- Dva lidé mají společné tajemství a musí si poslat nějakým způsobem tajné informace.
- Špión chce vaše informace zjistit, proto si musíte posílat zašifrované dopisy, kterým rozumíte jenom vy a ten, kterému je posíláte.
- Dáte informaci do truhly a použijete na její uzamčení zámek, který zakódujete – šifrování.
- Druhá osoba tuto truhlu dostane a použije k otevření s vámi dohodnutý kód – dešifrování. I kdyby se dostaly informace ke špiónovi, tak není schopen jim porozumět.
Caesarova šifra
Jak tato šifra fungovala ?
- Caesar posunul každé písmeno v jeho příkazech, aby pro nepřítele nedávaly smysl.
- Například: Dohodnu se s kamarádem, jaký posun použijeme. Pokud vybereme 3 posuny, tak písmeno A nahradíme písmenem D, písmeno C nahradíme F atd..
- Zprávu kamarád vyluští tak, že posune každé písmeno o tři zpátky v abecedě.
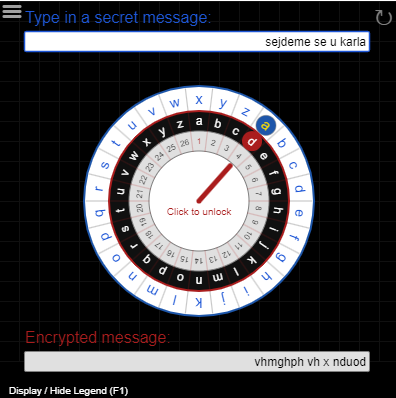
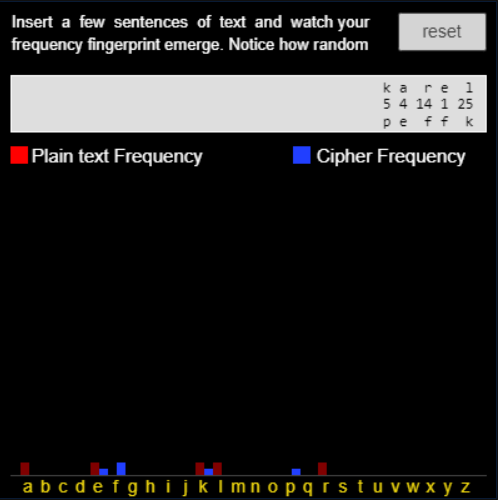
Prolomení této šifry pomocí frekvenční analýzy
- Alkindus prolomil Caesarovu šifru tím, že využil důležité vlastnosti jazyka.
- Vezmete libovolnou knihu a spočítáte výskyt každého písmene, tak najdete podobný vzorec.
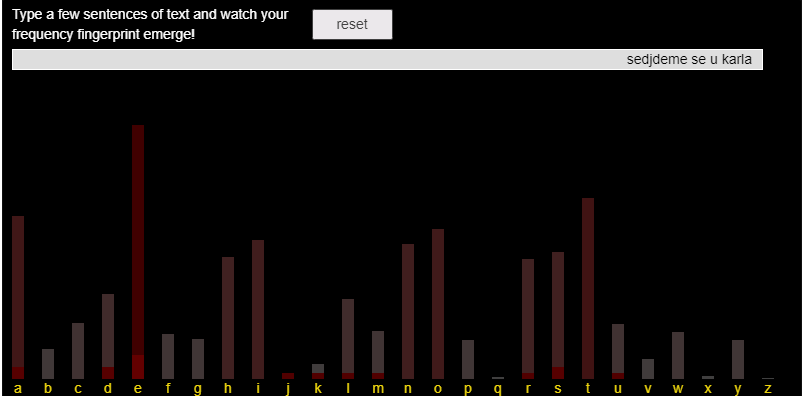
- Můžete se na to dívat jako na otisk angličtiny. Tento otisk zanecháváme při komunikaci a ani si to neuvědomujeme.
- K prolomení této šifry stačí spočítat výskyt každého písmene v zašifrovaném textu a podívat se o kolik se otisk jazyka posunul.
- Pokud je v zašifrované zprávě nejčastější písmeno H namísto E, tak je posun pravděpodobně 3. Stačí tedy posun obrátit a odhalíme původní zprávu.
Polyalfabetická šifra
Co to je za šifru?
- S mým kamarádem máme společné tajné slovo, to znamená, že změním kódové slovo na čísla podle pořadí jednotlivých písmen v abecedě. Tuto posloupnost zopakujeme pod zprávou.
- K zašifrování používáme více posunů než jeden na rozdíl od Caesarovy šifry.
- K dešifrování můj kamarád zprávu poskládá zpětným posunutím podle kódového slova.
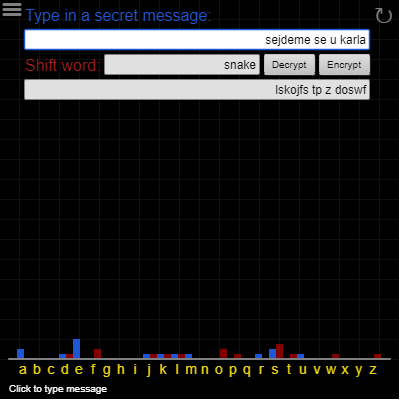
Jak prolomit tuto šifru?
- Odposlouchávající hledá nějakou informaci, která oslabí šifru, jakýsi částečný otisk prstu.
- Vždy, když je rozdíl mezi četností písmen, tak dochází k úniku informace. Tento rozdíl je způsobený opakováním v zašifrované zprávě.
- Aby prolomili šifru, musí zjistit délku kódového slova.
- Budou muset zkoušet frekvenční zastoupení písmen pro různé intervaly. Když si vezme frekvenční zastoupení pro každé páté písmeno, objeví otisk prstu.
- Jejich úkol je rozluštit 5 samostatných Caesarových šifer ukrytých v opakující se frekvenci.
- Silou polyalfabetické šifry je tedy čas, který je potřebný na zjištění délky kódového slova. Čím delší kódové slovo, tím silnější šifra.
Neprolomitelná Vernamova šifra
Na jakém principu tato šifra funguje?
- Odpovědí je princip náhody
- Představme si, že házím 26-stěnnou kostkou, abych vytvořil seznam náhodných posunů k zašifrování zprávy.
- Důležité je, aby seznam byl stejně dlouhý jako zpráva, aby se vyhnula opakování.
- Kamarád Bob ji rozšifruje pomoci stejného seznamu posunů, který jsem mu předal.

Jak velká síla této šifry doopravdy je ?
- Abychom si ukázali sílu této šifry, musíme pochopit množství kombinací, které tu je.
- Například Caesarova šifra posouvala každé písmeno o stejné číslo mezi 1 a 26. To je malý počet možností. Všechny se dají lehce zkusit.
- Představme si, kolik možností zašifrování teď existuje. Je to 26 na pátou, což je téměř 12 milionů.
- Kdybych napsal své jméno na jeden list papíru a na něj dal hromadu papírů se všemi možnými zašifrováními, jak vysoká hromada by to byla? S 12 miliony kombinacemi pěti písmen by tato hromada byla obrovská. Vysoká přes 1 kilometr.
- Když zašifruji své jméno Vernamovou šifrou, je to jako bych si náhodně vybral jednu stránku z této hromady. Toto je bezchybné zabezpečení v praxi.
Frekvenční stabilita
Představte si 2 místnosti. V každé místnosti je vypínač. V jedné místnosti je muž, který vypínačem přepíná podle hodu mince. Když padne líc, vypínač zapne. Když rub, tak ho vypne. V druhé místnosti přepíná světlo žena podle slepého odhadu. Snaží se napodobit náhodnost bez mince.
- Potom pustíme hodiny, aby začaly přepínat ve stejném čase.
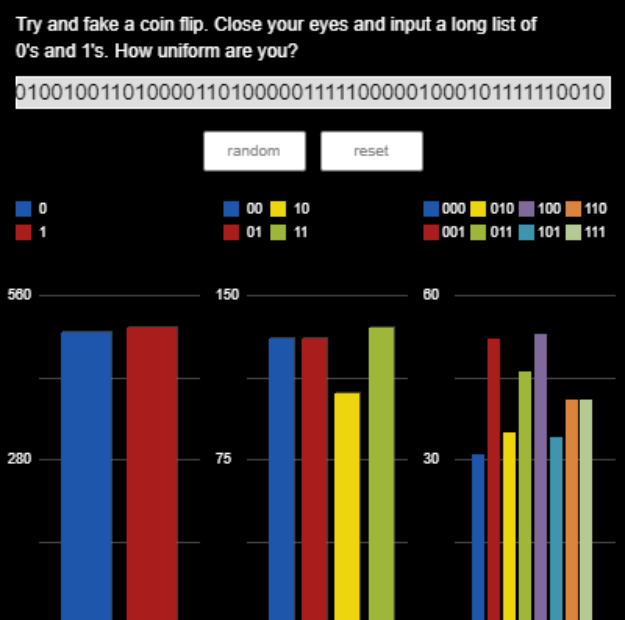
Můžete určit, která žárovka se zapíná podle hodů mince?
- Finta je v tom, že se musíte podívat na vlastnosti každé posloupnosti, ne na určité vzory.
- Například můžeme zkusit spočítat všechny jedničky a nuly, které se v posloupnosti objevují.
- Toto však nestačí, protože je jich zhruba stejně. Pomůže nám spočítat všechny menší posloupnosti.
- Například série tří po sobě jdoucích přepnutí. Když je posloupnost skutečně náhodná, tak bude obsahovat zhruba stejný počet všech posloupností libovolné délky. To se nazývá frekvenční stabilita.

- Lidé totiž upřednostňují jisté posloupnosti, když tipují. To vede k nerovnoměrnému rozložení jako to, které vidíme nahoře.
- Když budeme mincí házet 10x, tak je stejně pravděpodobné, že padne 10 rubů, 10 líců, nebo jakákoliv jiná možná posloupnost.
Šifrovací stroj Enigma
Od toho okamžiku mohly být informace převáděny do podoby elektrických pulzů a předávány po celém světě téměř mžiknutím oka.
- Převody akcií a peněz, to byly komerční služby, které předznamenaly novou éru celosvětové komunikace.
Dřívější rotační šifrovací stroj
Nejprve si vezmeme dva totožné stroje a dohodneme se na jejich počátečním nastavení, které nazýváme klíč. Provedeme řadu stejných činností, abychom docílili stejných výsledků.
Například zpráva „Attack northwest“ (zaútočte severozápadně) by byla zašifrována následovně:
- Se třemi rotory, každý po 26 číslech, by se posloupnost začala znovu opakovat po 26x26x26. To je stejné, jako byste měli seznam posunů v abecedě čítající 17 576 čísel.

Zkusme si teď prostor klíčů znázornit.
- Nejprve si zvolíme jedno z šesti možných uspořádání rotorů. Pak vybereme počáteční nastavení rotorů. Dostáváme tak prostor klíčů čítající více než 100.000 prvků.
- Uvědomte si, že každá konfigurace stroje je bodem tohoto prostoru. Když zvolíme klíč, vybíráme počáteční bod z tohoto prostoru, který určuje pořadí následných posunů v abecedě.
- Prozradíme-li klíč, pak jsme prozradili celou posloupnost.
Generátory pseudonáhodných čísel
Skutečně náhodná čísla můžeme získat měřením tohoto kolísání, kterému se říká šum.

- Měřením šumu, přesněji řečeno jeho vzorkováním, můžeme získat čísla. Například měřením elektrického proudu televizního šumu v průběhu času získáme posloupnost skutečně náhodných čísel.
- Tuto posloupnost můžeme zobrazit jako cestu, která mění směr podle každého čísla. Tomu se říká ‚random walk‘ (náhodná procházka).
- Říká se, že náhodné procesy jsou nedeterministické, protože se nedají determinovat (předpovědět) dopředu.
- Stroje jsou naopak deterministické. Jejich fungování je předvídatelné a opakovatelné.
Neumann vytvořil algoritmus, aby mechanicky simuloval náhodnost. Nejdříve vybral skutečně náhodné číslo, zvané ‚seed‘ (semínko).
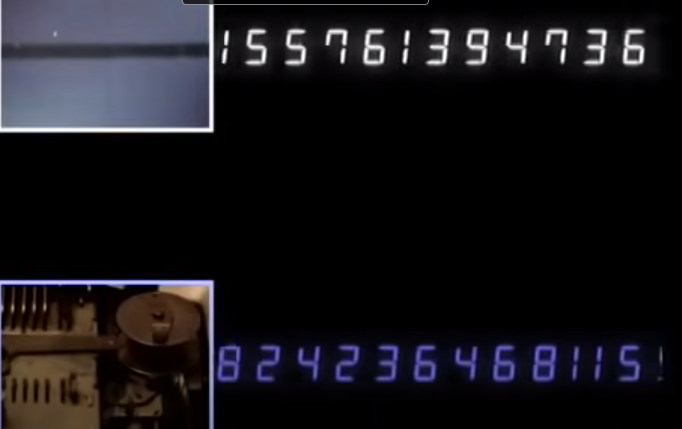
Toto číslo můžeme získat například měřením šumu nebo aktuálního času v milisekundách.
Semínko se umocní a výstupem bude prostřední část výsledku. Tento výstup se použije jako nové semínko, a to se opakuje kolikrát je potřeba. Toto je známé jako ‚Middle-square method‘.
- Vypadají podobně, dokud nezrychlíme. Pseudonáhodná sekvence se po čase začne opakovat. Toto se stává, když algoritmus použije semínko, který už použil, a proto se bude cyklus opakovat.
- Délka, po které se posloupnost bude opakovat, se nazývá perioda. Perioda závisí na délce počátečního semínka.

Když použijeme dvojciferné semínko, může algoritmus vytvořit nejvíce 100 čísel před novým použitím semínka a opakováním cyklu.
Při trojciferném semínku se cyklus může opakovat až po 1000 číslech.
A u čtyřciferného semínka to může být až 10 000 čísel bez opakování.
Kdybychom tedy použili dost velké semínko, posloupnost může mít biliony a biliony čísel bez opakování.

– U pseudonáhodných generátorů se bezpečnost zvyšuje s větší délkou semínka. Kdyby i nejvýkonnějšímu počítači trvalo stovky let, než projde všechna semínka, můžeme říci, že je to prakticky bezpečné, i když ne dokonale bezpečné.
Tím, že se počítače zrychlují, se musí zvyšovat i velikost semínka.
